, derive the
conservation law:
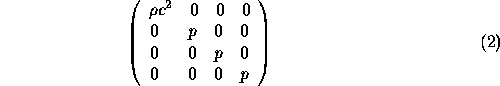
in the momentarily comoving reference frame [ MCRF ]. By applying a Lorentz transformation , show that in a general frame it is given by
Prove that the time and space parts of the conservation equations
in the MCRF are
and
and derive the Newtonian limit of these equations. [ This is just filling in the algebra of the derivation in section 4.1 of the lecture Notes.]
and the current four- vector 
given
in the lectures, show that Maxwell's equations can be written as
and
Perform a Lorentz transformation on 
to a frame
with velocity v in the x- direction to prove that
the part of the electric field perpendicular to
changes to 
, while the part along
is unchanged.
is
Express its components in terms of 
, 
and
the three- velocity 
. By writing
and using Maxwell's equations, show
that
where
is the energy- momentum tensor of the electromagnetic
field. Infer that the energy density is
NOTE: This question is worth a bottle of wine!!!
, moves in a circular
orbit of radius R in a uniform B field 
.
(5a) Find B in terms of R, q, and 
, the angular frequency.
(5b) The speed of the particle is constant since the B field can do no
work on the particle. An observer moving at velocity 
, however, does not see the speed as a constant. What is 
measured by this observer?
(5c) Calculate 
and thus 
. Explain
how the energy of the particle can change since the B field does no work
on it.
If you have any problems please come and see me or contact me by
email.
